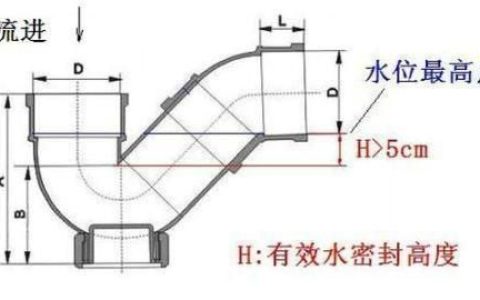
展现数学之美的病态函数
试想一个场景:
有一根细线,
它是无限长的,或者说要多长有多长,
这根线,自始至终都是连续的,从左到右不曾间断。
比如这根弧线:
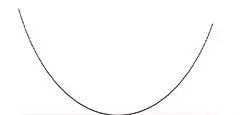
弧线底部的水平直线,就是弧线的切线。
所谓切线,就是恰好与弧线在切点附近,有且仅有切点这一个交点。
有切线的地方,说明弧线在这附近是光滑的,是没有尖刺的。
如果弧线每一点都有切线(可导),说明弧线处处都光滑。

如上图,如果“弧线”变成尖锐的“折线”,那么,“折点”处就有很多根直线与其只有一个交点,从数学上来说,折点的切线的斜率左右极限是不同的,因此这一点也没有“切线”。
即,折点不是光滑的,它是“尖锐的”,曲线在这一点是不可导的。
当然,如果面条在某处断了,在断点处,也是没有切线的,也是“尖锐粗糙的”。
那么,有没有一种既连续、不曾间断,却每一点都尖锐的线呢?
用数学语言描述即:
是否存在处处连续,却处处不可导的函数?
直觉上来说,一根连续曲线的尖锐点至多是可数的,有限的。
因为一根连续的线,再怎么折,尖锐的部分也应该是有限的,而光滑的、平直的部分是占大多数的。
在尖刺的旁边,我们总是应该可以找到哪怕一小段平滑的部分。
在数学发展史上,数学家们也一直猜测:连续的函数必然是近乎可导的(即:起码有一些光滑的部分),所谓不可导的点也必然只占整体的一小部分。连续函数在其定义域中,应该是除去有限个点外都是可导的。
一根线不可能处处都尖锐吧?
1872年,德国数学家魏尔斯特拉斯(集合论大师康托尔的导师)利用函数项级数构造出了一个病态函数,为上述猜测做了一个终结,函数数学描述如下:
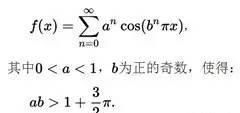
这个函数逆天在于,
它处处连续,却又处处不可导
简而言之,它的尖刺折点是如此之多,以至于无论你放多大,在多细微的尺度观察任何一段,函数图像都不会显得更加光滑,它处处都是尖锐的。
这怎么可能?
它的证明首次出现在魏尔斯特拉斯于1872在普鲁士科学院出版的一篇论文中,我们现在称它为魏尔斯特拉斯函数。
说它病态,是因为它是一种不可测函数。
你无法用笔画出任何一部分图像的函数,因为每一点的导数都不存在,画的人将无法知道每一点该朝哪个方向画。
通过计算机逐点描绘,函数图像是这样的:
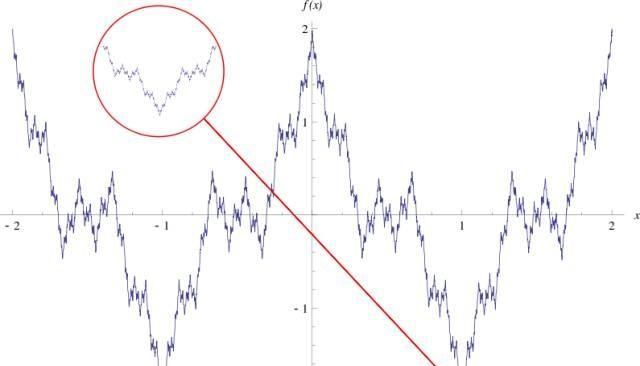
该反例构造出来后,在数学界引起极大的震动。
因为对于此类病态函数,传统的数学方法已无能为力。这个发现以及后来许多病态函数的例子,充分说明了直观及几何的思考不可靠,而必须诉诸严格的概念及推理。
随后,这个例子促成了一门新的学科“分形几何”的产生。所谓“分形”,就是指某图案的局部与整体具有相似性。这种性质又称为“自相似”。
反常的病态函数是极少数特例吗?
分析学的成果表明,尽管它们“反常”,但病态函数事实上不在“少数”,甚至比那些“健康”的函数“多得多”。
例如:
狄利克雷函数——定义在整个连续实数域(-∞, +∞),却处处不连续;
爆米花函数(Thomae’s function)——处处极限为0,但在任意小区间中,都包含着无数个值不为0的点。
必须要指出,类似魏尔斯特拉斯函数的例子历史上并不是老魏第一个提出的。
在他之前,数学分析严谨化的另一位推动者——捷克数学家波尔查诺,在他1834年撰写但未完成的著作《函数论》中,首次给出了一个处处连续但处处不可导函数的例子,但他并未给出函数的解析表达式,且遗憾的是,他的贡献多半被他的同时代的人所忽视,许多成果若干年后才被发现,但功劳已被抢占或只能与别人分享了。
诺诺心里苦啊!
直觉不一定科学
你看,经过几千年的进化,人类自身还是倾向于相信直觉,“所见即所得”在大多数情况下依然相当有说服力。比如下面这些看起来都像是天然正确、不容置疑的:
-
光线永远是沿直线传播的;
-
任何地方的时间是同步的;
-
只要不断加速,物体的速度是没有限制的。
幸好,我们还有数学。
————————————————–
原创文章,作者:小编,如若转载,请注明出处:http://www.ranqigaiguan.com/yhtg/15269.html